Instructor:   Dr. Brian Jewett Office:   Atmos. Sci. Bldg room 201 Phone:   (217) 333-3957 E-mail:   bjewett@illinois.edu Days/Time:   12:30-1:50pm Tu/Th Location:   Siebel Center room 1304 Credit, CRN:   4 hours; 37123, 37126 Prerequisites:   MATH 241 or consent of instructor   click for handout; or view this PNG

Right: Visualization of final course problems from recent years.

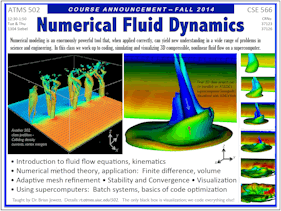
click either animation for full-sized movie   Shown on left: (1) surface Y-component winds (shaded, and vectors); (2) potential temperature surface showing colliding density currents; (3) vertical velocity (red +, blue -) mapped onto ~0.1/sec vertical vorticity surface. There are +Y winds (orange) in the right half of the domain, and -Y (blue) in the left. A vortex sheet develops between colliding density currents. Small perturbations grow and vorticity is stretched as convergence and vertical motion concentrate near the center axis. Merging of nearby vortices results in upscale growth to fewer, larger rotation centers before the solution decays. On Right: Movie of last year's problem, seen with VisIt. View is ~towards -X, of isosurface of perturbation potential temperature, with color along the surface representing vertical motion (scale runs -15 to +15 m/s). A cold thermal descends to the surface ahead of a descending density current. Shear of the Y-flow component between the density current, environment, and cold thermal leads to a rolling up of the vortex sheet, and significant vorticity as it interacts with the isolated cold source. (Computation, parallelization and visualization were all parts of the grade).

FOR: This course is for those interested in numerically solving partial differential equations that describe
          compressible fluid flow, utilizing a high performance production XSEDE supercomputer, likely Stampede.

KEY OBJECTIVES: that those taking the course leave it with -

1. A thorough understanding of the fundamentals - the basis for choosing and evaluating numerical methods
2. The ability to critically interpret numerical methods as presented in the literature. We will work through several papers and examine their descriptions of their methods and how they are assessed in terms of stability, accuracy, and error characteristics
3. Most important: the ability to apply these methods to high-performance computers. There will be no "black boxes" (other than visualization packages) in the course - the emphasis is on coding and understanding numerical method behavior as applied to linear and nonlinear fluid flow problems in 1-D, 2-D and ultimately 3-D settings.
4. Consequence of the above: That by the end of the course you are very comfortable with, and capable of effectively using, supercomputer-class facilities. This includes writing and debugging code, compiling and running it, and visualizing your results. Along these lines, you will use the "old, slow" way of coding problems, along with newer development environments (IDEs) that are the future.

COMPUTER PROBLEMS: We will use the XSEDE Stampede supercomputer to solve fluid flow problems in one, two and three dimensions, using regular and nested grid approaches. I will emphasize writing clear and effective programs, as well as (a bit of) structuring codes for efficient use of parallel computers. Course assignments may be programmed in either Fortran 90 or C, and introductory codes and plotting programs in both languages will be provided. The behavior of the numerical solutions will be compared to known solutions when they are available.

The computing objectives are (a) getting everyone comfortable and familiar with our programming environment on a production supercomputer, (b) getting started with 1-D codes before we add complexity, and (c) working up to 3-D nonhydrostatic nonlinear problems by the end of class. Each class computer problem will be designed to build on the last to make understanding and completing the assignments more straightforward for all.

PROGRAMMING EXPERIENCE: You should be comfortable with a programming language, or ready to learn. This class could be abrupt if you have no programming experience at all, as we get going fairly quickly. To help everyone get started and to begin at a common starting point, I will pass out an introduction (sample) program at the start of class (in Fortran 90 and also in C) which will serve as a basis upon which you will build your later programs. For those rusty in F90 or C (or Linux), there will be review sessions early in the semester. However, you might want to consider taking one of the many classes offered by the University's Computer Science and/or CSE departments to strengthen your programming skills. The goal here is using a programming language, rather than learning one.

If you feel your programming experience is not very strong and you want to do some preparation before class starts, I recommend the following:

• Fortran: textbook (PDFs free at UI library online), tutorials and other references
• C: an inexpensive textbook, tutorials and other references
• Linux: Linux info, text editors

TEXT: There is no single textbook now. I will use books (there are many) whose material is available free as PDFs online from the UI library.

INTRO: Welcome; I am Dr. Brian Jewett. I teach and carry out research in the Atmospheric Sciences Dept. My specialty is 3d numerical modeling of a variety of atmospheric phenomena - severe thunderstorms and squall lines, hurricanes, and snowstorms.

If you have any questions about the class, please feel free to contact me.

And remember, fluid modeling and visualization is fun! (here's another one).